3. Chaos
Chaotic systems
- deterministic systems with statistical behavior similar to stochastic processes
- can be discrete or continuous in time
- yield insights to dynamical origins of statistical behavior measured time series
Maps
\[x_{t+1} = f(x_{t},t)\]Autonomous if \[f=f(x)\]
Bernoulli map
\[x_{t+1}=2x_{t} \mbox{ mod } 1\]
https://upload.wikimedia.org/wikipedia/commons/6/68/Exampleergodicmap.svg
- stretch-and-fold
- binary code for numbers \[ z = \sum_{t=0}^\infty \frac{b_t}{2^{t+1}} \]
- rational numbers: periodic
- irrational numbers: generally infinite series
Bernoulli map
\[x_{t+1}=2x_{t} \mbox{ mod } 1\]
- Pseudo-random numbers: see exercise
Measure preserving maps F
\[ \int f(Fx) \rho(x) \mathrm{d}x = \int f(x) \rho(x) \mathrm{d}x \]Nondecomposable maps F
\[ FA = A \Rightarrow \int_A \rho(x) dx = 0 \mbox{ or } 1 \; \; \forall A\]Mixing maps F
\[\lim_{n\rightarrow\infty} \rho(F^{n}A\cap B) = \rho(A) \rho(B) \ \ \ \ \forall A,B\]- For measure-preserving maps: \[\mbox{Nondecomposable} \Rightarrow \mbox{Mixing}\]
Ergodic maps
A map T is ergodic if
\[\lim_{N\rightarrow \infty} \frac{1}{N} \sum_{n=0}^{N-1} f(F^nx) = \int\mathrm{d}\rho f(x)\]for almost all orbits and arbitrary measureable f
- Measure preserving and nondecomposable maps are ergodic
e.g. the Mean Squared Displacement in ergodic systems can be replaced by the time average:
\[ \langle (x(t)-x(0))^2 \rangle = \langle \frac{1}{T-t} \int_{0}^{T-t} \mathrm{d}t^\prime (x(t^\prime+t)-x(t^\prime))^2 \rangle \]or, in discrete time,
\[ \langle (x(t)-x(0))^2 \rangle = \langle \frac{1}{T-t} \sum_{t^\prime=1}^{T-t} (x(t^\prime+t)-x(t^\prime))^2 \rangle. \]Lyapunov Exponents
https://en.wikipedia.org/wiki/Lyapunov_exponent#/media/File:Orbital_instability_(Lyapunov_exponent).png
- Chaotic systems exhibit sensitive dependence on initial conditions
- Exponential approximation of escape of two nearby points \[ \left|F^t(x_0+\epsilon) - F^t(x_0)\right| \approx \epsilon e^{t\lambda(x_0)} \]
- The Lyapunov exponent is defined for each initial point \[ \lambda (x_0) = \lim_{t\rightarrow \infty} \frac{1}{t} \sum_{n=1}^{t} \log|F^\prime(x_n)| \]
Fixed Points
\[ x_f=F(x_f) \]Look at environment
\[ [ x_f-\epsilon, x_f+\epsilon ] \] \[\delta_{t+1} = |x_{t+1}-x_f|=|F(x_f\pm \delta_t)-x_f|=\delta_t \left|\frac{F(x_f\pm\delta_t)-F(x_f)}{\delta_t}\right|=\delta_t|F^\prime(x_f)|\]Logistic map
\[x_{t+1}=rx_{t}(1-x_{t}) \]Fixed points?
\[ x_f = r x_f ( 1 - x_f ) = r x_f - rx_f^2 \] \[ rx_f^2 + (1-r) x_f = 0 \] \[ {x_f}_1 = 0 \; \; \; \; \; {x_f}_2 = \frac{r-1}{r} \]Stability?
\[ F^\prime (x_f) = r (1-2x_f) = 2-r \]
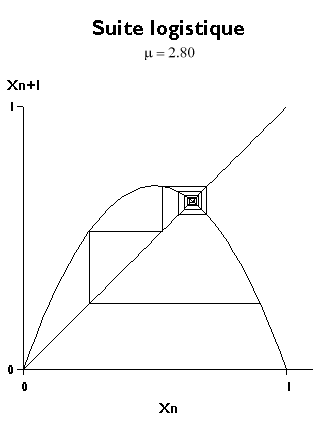
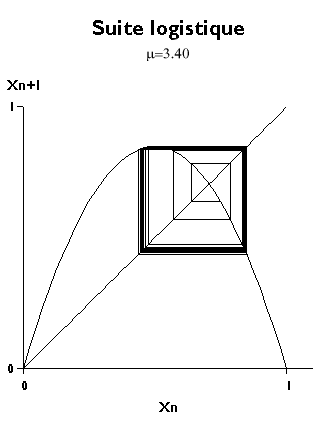
https://fr.wikipedia.org/wiki/Suite_logistique
- Number and types of fixed points depend on r
Bifurcations
https://upload.wikimedia.org/wikipedia/commons/thumb/5/50/Logistic_Bifurcation_map_High_Resolution.png/800px-Logistic_Bifurcation_map_High_Resolution.png
The pendulum
\[\ddot{\theta} + g \sin(\theta) =0\]It can be rewritten as
\[\dot{\theta}=p\] \[\dot{p}=-g\sin(\theta)\]The damped pendulum
\[\ddot{\theta} + \gamma \dot{\theta} + g \sin(\theta) = 0 \]In phase space
\[ \dot \theta = p \] \[ \dot p = -\gamma p - g \sin(\theta) \]- decays to zero
The driven pendulum
\[\ddot{\theta} + \gamma \dot{\theta} + g \sin(\theta) = A\cos(\omega t) \]In phase space
\[ \dot \theta = p \] \[ \dot p = -\gamma p - g \sin(\theta) + A\cos(\omega t) \] simulation