Biological Physics Group
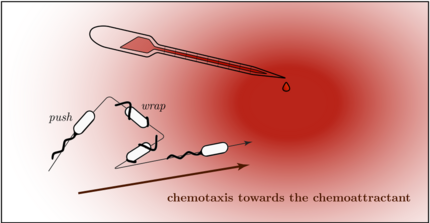
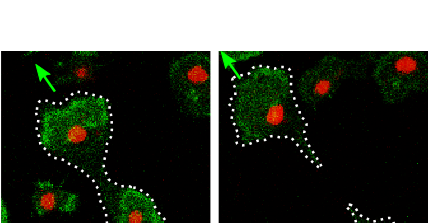
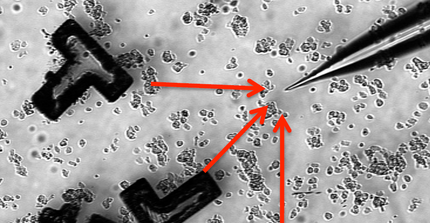
Ranging from the molecular and cellular scale to tissues, organisms, and whole ecosystems, the complexity of living systems poses some of the most fundamental challenges to current scientific research. In the Biological Physics Group, we focus on the level of individual cells, where we address biological questions with the tools of physics, relying, in particular, on microscopy and micromanipulation techniques as well as on the ideas and concepts of pattern formation in nonlinear systems.